I am sure you have seen Venn diagrams before. Venn diagrams are amazing — they can represent complex relationships between sets in a rather intuitive way. And it does not matter what these sets represent. If you are working with sets, you will often find Venn diagrams to be a natural way to present your data. But it so happens that this is generally because we are working with two or three sets at a time, or because the relationships between our sets are somewhat simple. This is what I discovered recently.
I will present a concrete example to illustrate my discovery. A very frequent problem in high school set theory is to find the number of elements in some union or intersection of two or three sets. I have often used Venn diagrams like those below to visualize the data provided in such problems, and then solve them.
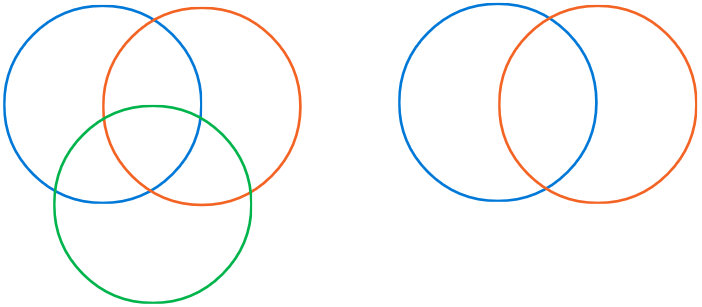
Occasionally, the problem at hand would seemingly involve more than three sets1 and I would try to extend the same technique to the following “Venn diagram”.

Unsurprisingly2 I remember that this would often not work! I would not get the correct answer and would eventually end up having to either simplify the problem to three sets, somehow brute force my way to answer or just find a different approach3. Now, I know that this was because the above “Venn diagram” is not a Venn diagram at all! An easy sanity check that I should have done is to count the number of regions in the diagram. For four sets, I must have had \(2^4 = 16\) regions, but the diagram above has only \(14\). It is not possible to create a Venn diagram for four sets using circles in the first place!
This is not a mathematics blog and so I would not delve into too many details, but here is one way to think about this. Two circles can intersect at at most two points. Each intersection between two circles creates one new region4. So if I have \(n\) circles, adding another creates at most \(2n\) new regions. Solving this recurrence5 tells us that we can create at most \(2 + n(n-1)\) regions with \(n\) circles. As you can see, this is outgrown by the desired \(2^n\) after \(n = 3\).
Suppose we do not restrict ourselves to circles, and take another shape that can intersect with another copy of itself in at most \(k\) points. Then adding the \(n+1\)-th shape creates at most \(kn\) new regions, and we can create at most \(2 + kn(n-1)/2\) regions with \(n\) copies of the shape. A simple internet search will tell you that one can use ellipses to create Venn diagrams for four sets. Note that ellipses can intersect at up to \(4\) points, and so \(n\) ellipses can create at most \(2 + 2n(n-1)\) regions — which is overtaken by \(2^n\) only after \(n = 5\). As you might be able to see, our quadratic terms will always eventually be overtaken by the exponential \(2^n\) and so no finite set of shapes can create a Venn diagram for an arbitrary number of sets!
Keeping aside the above jargon, let me mention that when I discovered this, I was not trying to make a full-fledged Venn diagram for four sets. I was preparing a presentation about Code Translation6 and wanted to show that it lies at the intersection of four different areas in software engineering. I thought I could draw something like the flawed four-set “Venn diagram” above, but I couldn’t get it to come up neatly. I searched on the internet for examples of Venn diagrams with four sets and came to realize that I knew little about Venn diagrams all this time. Nonetheless, this is what I ultimately drew7.
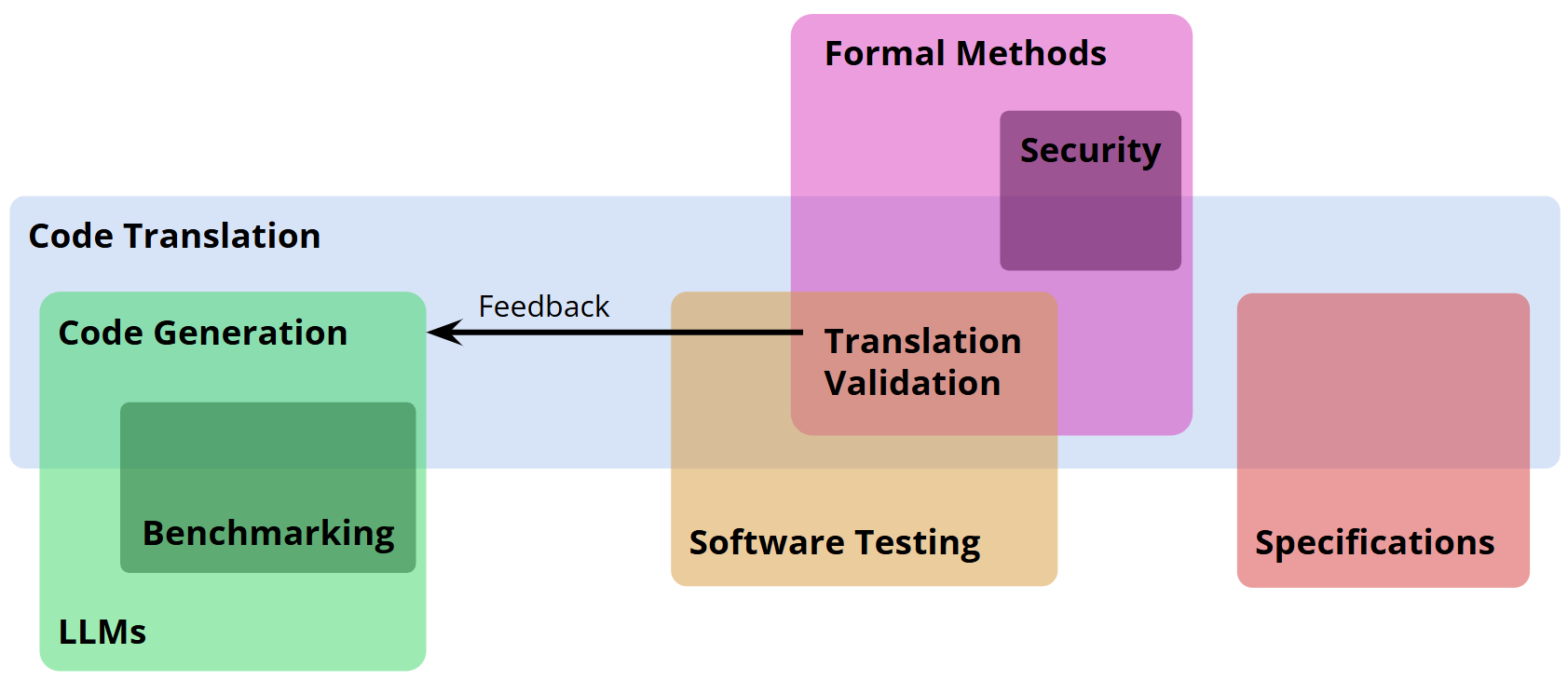
-
I only remember the case of four sets. ↩
-
Unsurprising only recently. ↩
-
I probably also gave up on some problems. ↩
-
This may or may not be intuitive, but I leave it as an exercise to the reader to prove this. 😉 ↩
-
Again, I leave this as an exercise to the reader. ↩
-
From one programming language to another. 🥁 A post about code translation might be on its way! 🥁 ↩
-
I know that this is not a Venn diagram but rather an Euler diagram — please spare me some liberty here. ↩